Tree는 단순한 데이터의 저장이 아닌 "데이터의 표현을 위한 도구"이다.
자료구조를 공부하는데 있어서 시야를 넓게 가지고 깊게 사고하려는 노력이 필요하다. 좁은 시야에서 다 이해했다고 착각은 금물

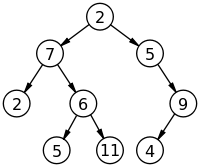
이진 트리의 조건
: 루트 노드를 중심으로 두 개의 서브 트리로 나뉘어짐 (empty set도 node로 간주)
나뉘어진 두 서브 트리도 모두 이진트리
이러한 특성에서 그 구조가 재귀적임을 보인다.
Tree의 level과 높이
각 노드의 깊이(depth)는 루트 노드에서 자신까지 가는 경로의 길이이다.
트리의 특정 깊이를 가지는 노드의 집합을 레벨(level)이라 부르기도 한다. 루트 노드의 깊이는 0이다.
트리의 높이(height)는 루트 노드에서 가장 깊이 있는 노드까지 가는 경로의 길이이다. 루트 노드만 있는 트리의 높이는 0이다.
full binary tree(정 이진 트리)
leaf node(자식이 없는 노드)가 아닌 모든 노드가 2개의 자식을 가진 트리이다.
complete binary tree(완전 이진 트리)
위에서 아래로 왼쪽에서 오른쪽으로 채워진 트리를 말한다.
끝 부분(마지막 레벨)을 제외하고 모든 노드가 채워진(마지막 레벨을 제외하고는 모든 노드가 자식노드를 2개를 가진) 이진 트리.
마지막 레벨의 노드들은 왼쪽으로 채워져 있다. 마지막 레벨이 다 채워질 수도 있다.
perfect binary tree(포화 이진 트리)
모든 단말 노드의 깊이가 같은 정 이진 트리이다.
동시에 complete binary tree이기도 하다. (모든 레벨에 노드가 꽉 차야하므로, 역은 성립하지 않음)
이진 트리 구현의 두가지 방법
배열 기반, 이진 트리
위에서 아래, 왼쪽에서 오른쪽으로 노드에 번호를 부여
양방향 연결리스트 기반, 이진트리
실제 구현
하나의 노드는 그 자체로 이진 트리 (entry set도 node이다)
따라서 노드를 표현한 구조체는 실제로 이진 트리를 표현한 구조체가 된다.
// 노드를 표현한 구조체
typedef struct _bTreeNode
{
BTData data;
struct _bTreeNode * left;
struct _bTreeNode * right;
}BtreeNode;
이진 트리의 모든 노드는 직/간접적으로 연결되어 있으며
루트 노드의 주소 값만 기억하면 이진 트리 전체를 가리키는 것과 다름 없다.
헤더파일에 선언되는 함수들
BTreeNode * MakeBTreeNode(void); // 노드 생성
BTData GetData(BTreeNode * bt); // 노드에 저장된 데이터 반환
void SetData(BtreeNode * bt, BTData data); // 노드에 데이터 저장
노드에는 함수를 통한 접근이 좋다.
하나의 노드도 이진 트리란 사실을 인지.
BTreeNode * GetLeftSubTree(BTreeNode * bt); // 왼쪽 서브 트리 주소값 반환
BTreeNode * GetRightSubTree(BTreeNode * bt); // 오른쪽 서브 트리 주소값 반환

void MakeLeftSubTree(BTreeNode * main, BTreeNode * sub); // main의 왼쪽 서브트리로 sub 연결
void MakeRightSubTree(BTreeNode * main, BTreeNode * sub); // main의 오른쪽 서브트리로 sub 연결
위의 함수는 노드 뿐만 아니라 트리를 대상으로도 적용되는 함수들이다.
이진트리를 생성하는 main함수 예
int main(void)
{
BTreeNode * ndA = MakeBTreeNode();
BTreeNode * ndB = MakeBTreeNode();
BTreeNode * ndC = MakeBTreeNode(); // 노드 A, B, B 생성
SetData(ndA, 1);
SetData(ndB, 2);
SetData(ndB, 3);
MakeLeftSubTree(bt1, bt2); // 노드A의 왼쪽 자식 노드로 노드 B 연결
MakeRightSubTree(bt1, bt3); // 노드A의 오른쪽 자식 노드로 노드 C 연결
( ... )
}
'코스웨어 > 16년 스마트컨트롤러' 카테고리의 다른 글
| 2016-09-22_조재찬_스터디일지_CPP-Class (0) | 2016.09.23 |
|---|---|
| 2016-09-21_조재찬_스터디일지_C++기초 3 (bool, reference, new&delete, C 표준함수 호출) (0) | 2016.09.21 |
| 2016-09-20_조재찬_스터디일지_C++기초 2 (기초예제, inline함수, namespace) (0) | 2016.09.20 |
| 2016-09-12_조재찬_스터디일지_C언어-이진 트리의 구현과 순회(Traversal) (0) | 2016.09.13 |
| 2016-09-09_조재찬_스터디일지_C언어-Doubly Linked List (0) | 2016.09.09 |
| 2016-09-08_조재찬_스터디일지_C언어-Circular Linked List (0) | 2016.09.08 |
| 2016-09-07_조재찬_스터디일지_C언어-연결리스트의 정렬삽입 (0) | 2016.09.08 |
| 2016-09-07_조재찬_스터디일지_C언어-Linked List (0) | 2016.09.08 |








