정렬알고리즘이 하나도 기억이 안나서 ㅡㅠ 새로 공부하는김에 겸사겸사 올려염 ㅠ
1. 버블정렬이란?
- 인접해 있는 두 개의 값을 비교해서 자료 교환을 한다.
- 오름차순 정렬은 두 개의 값을 비교해서 큰 값을 오른쪽으로 보내는 방식이다,
내림차순 정렬은 두 개의 값을 비교해서 작은 값을 오른쪽으로 보내는
방식이다.
2. 버블정렬을 이용하여 오름차순으로 정렬하는 그림

4. 버블정렬의 비교회수
-.
비교 회수 공식 : N(N –
1)/2
-.
위의 그림을 보시면 아시겠지만 제일
처음에는 (N – 1)번을 비교하고,
그 다음에는 (N – 2)번
만큼 비교하고, 그 다음은 (N – 3)번을 비교하면서
비교회수가 1이 될
때까지 이 작업을 반복할 것이다.
-.
비교회수는 (N –
1) + (N – 2) + (N – 3) …… + 1 이 될 것이다.
최대 (N – 1)번을 수행할
것이며, 각 패스가 수행할 때마다
수학식으로 표현하면 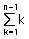
-. 5개의 값을 오름차순으로 버블정렬을 하면...
공식에 의해서 5(5 – 1)/2 = 10
가 성립된다.
즉, 총 10번의 비교를 통해서 오름차순으로 정렬된 값을 볼 수 있다.
5. 버블정렬의 연산시간
-. 연산시간 공식 :
O(n²)
-.
연산시간을 표기하는 방법은 일반적으로
사용하는 O표기법인데, 이
O표기법은 ‘최악의 경우’
(Worst Case)에 대한 연산시간을 나타낸다.
6. 버블정렬의 장점
-.
인접해 있는 두 개의 값을 비교하여 자료의 위치를
이동시키므로 단순하다.
-.
여러 차례 값을 비교하므로 안전성 있게 값을
정렬한다.
7. 버블정렬의 단점
-.
첫번째 패스에서 자료의 교환이 없었다면 주어진
값은 이미 오름차순으로 정렬된 상태이지만,
최대 N(N – 1)/2
만큼의 비교회수와 O(n²) 만큼의 연산시간이
소요된다.
-. 다른 정렬에 비해서 연산시간이 오래 걸린다.
8. 구현 예제
int bubble(int *arr, int arrSize)
{
int iCntI;
int iCntY;
int temp;
int cmpCnt = 0;
for( iCntI = 0; iCntI < arrSize - 1; ++iCntI )
{
for( iCntY = 0; iCntY < arrSize - 1 - iCntI; ++ iCntY)
{
++cmpCnt;
if( arr[iCntY] > arr[iCntY + 1] )
{
temp = arr[iCntY];
arr[iCntY] = arr[iCntY + 1];
arr[iCntY + 1] = temp;
}
}
}
return cmpCnt;
} 
9. 단점 보완
7번에서도 언급했듯이 정렬된 상태에서도 N(N – 1)/2 만큼의 비교를 한다는 것이다.
이점을 보완한 소스를 보자. 위의 소스와 동일하나 틀린부분만 글씨크고 굵게 표시하겠다.
int bubble(int *arr, int arrSize)
{
int iCntI;
int iCntY;
int temp;
int IsSorted;
int cmpCnt = 0;
for( iCntI = 0; iCntI < arrSize - 1; ++iCntI )
{
IsSorted = 1;
for( iCntY = 0; iCntY < arrSize - 1 - iCntI; ++ iCntY)
{
++cmpCnt;
if( arr[iCntY] > arr[iCntY + 1] )
{
IsSorted = 0;
temp = arr[iCntY];
arr[iCntY] = arr[iCntY + 1];
arr[iCntY + 1] = temp;
}
}
if( 1 == IsSorted )
break;
}
return cmpCnt;
} 

'기술자료 > C C++' 카테고리의 다른 글
| [賢斌] vector<벡터> - 3 (0) | 2009.08.13 |
|---|---|
| [賢斌] vector<벡터> - 2 (0) | 2009.08.13 |
| [오락실]선택정렬 (0) | 2009.08.13 |
| [賢斌] vector<벡터> (0) | 2009.08.13 |
| [賢彬] 변환 연산자들(Conversion Operators) (0) | 2009.08.12 |
| [賢彬] [무료제공 기술서적] Inside C#pdf 와 Source File (마이크로소프트 무료 배포판) (2) | 2009.08.12 |
| [賢彬] C Pointer and Arrays (0) | 2009.08.12 |
| [오락실]cout 으로 양식화된 출력 사용하기 (0) | 2009.08.12 |

